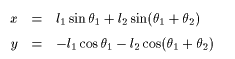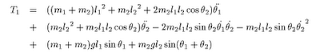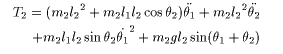2リンクマニピュレータの位置制御

以下のマニピュレータについて、次の二通りの制御方式を用いたシミュレーションを行った。

制御方式

1. 逆ヤコビ行列を用いた方法
2. 1に外乱オブザーバーを付加する方法

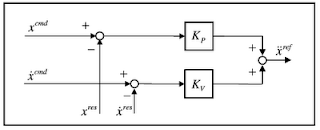
PD制御を用いており、システムのブロック図は以下のようになる。 ｖ

まず、理論を述べ、その後シミュレーション結果を載せる。

先端の目標軌道

• ステップ入力
• 円軌道

各パラメータには以下の値を用いた。

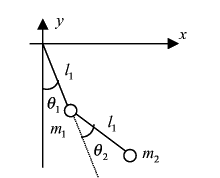
2リンクマニピュレータの動力学

動力学はマニピュレータの関節駆動力・関節初期位置から各リンクの位置・速度・加速度を求める順動力学問題と、各リンクの位置・速度・加速度及び作用力から各関節のモータが発生すべき関節駆動力を求める逆動力学問題がある．

順動力学はロボットの動作を表現するものとしてシミュレーションで必要となる．

逆動力学はロボット実機への制御入力を決定するために必要となる．一般のマニピュレータにおいて運動方程式は非常に複雑であるため、リアルタイム性が要求される実機の駆動においては影響の少ない項あるいは仕様に不必要な項を省略し計算を行っている．外乱オブザーバはこれらの省略項の影響を補償するものである．

動力学方程式(運動方程式)の導出方法としてはラグランジュ方程式による方法、ニュートンオイラー方程式による方法等があるが、ここではラグランジュ法によって導く．

ラグランジュ方程式の一般形

Robot Motionにおいてはニュートンオイラー法から運動方程式を求めているがここではラグランジュ方程式を用いて求める．

ラグランジュ関数Lは運動エネルギーKと保存エネルギーPとの差で定義される．

運動方程式はラグランジュ方程式で表される．

qiは各エネルギーを表現する一般化座標で、Fiはqiに依存した力あるいはトルクである．

ラグランジュ関数の導出

リンク1の運動エネルギーは次式で表される．

保存エネルギー（位置エネルギー）は次式のように求められる．

第2リンクの先端の座標を( x,y )とすると、θ1,θ2との関係は次のようになる．

以上の情報から、先端の速度が得られる。またリンク2の運動エネルギーK2、保存エネルギーP2が計算できる。
よってラグランジュ関数L = k-Pより導出が可能である。

動力学方程式の導出

動力学方程式導出のため、ラグランジュ方程式の各項を計算する.
Lをθ1の微分で編微分したもの、それをtで微分したもの、またLのθ1の微分したものの3つの関係式から関節1におけるモータのトルクが以下のように計算できる。（計算が結構めんどくさいので省略）

同様に関節2のモータのトルクを求める．

これらの式をまとめると以下のように表現できる

但し

ここで、慣性行列MにおいてMiiは自己慣性係数、Mijは相互慣性係数として知られる．非線形項Hの中で、Hijj(θj(の微分))^2項は関節ｊの速度により関節iに働く求心トルクである．またHiij(θi(の微分))^2(θj(の微分))^2はジョイントｊの速度によりジョイントiに働くコリオリ項である.Gは重力項を表している．

運動学

運動学はマニピュレータの先端の位置と、各関節の角度、角速度、角加速度とを結び付けるものである．運動学には順運動学と逆運動学がある．順運動学は各関節角から先端位置を一意に決定するものである．一方、逆運動学は先端位置より各関節角を定めるものであるが、その解は一意に存在するとは限らない．また、逆運動学は軌道計画の際に重要であり、目標軌道（通常直交座標空間におけるハンドあるいはマニピュレータ先端位置の軌道が計画される）を関節空間に変換する役割を持っている．

2リンクマニピュレータの順運動学

2×2の変換行列はヤコビ行列(Jacobian)と呼ばれる．速度と角速度の関係式は以下のように表すことができ、これは多自由度マニピュレータにも適用できる．ただし多自由度の場合はヤコビ行列は正則行列にならない．

上式を微分することにより、関節角速度と先端加速度を結び付ける関係式が得られる．

2リンクマニピュレータの逆運動学

余弦定理を用いることにより次式が得られる

先述したように、逆運動学問題では解が一意に求まらない．ここではθ1に2つの解が存在し、それぞれ肘を上げた、あるいは下げた姿勢に相当する．次に直交座標の速度から関節角速度を導出する．
加速度は逆ヤコビ行列より次のようになる．（速度も同様）

通常加速度における逆運動学は(37)~の第二項が第一項に比べ無視できることから次式のように近似して用いる．

逆ヤコビ行列を用いた制御方法

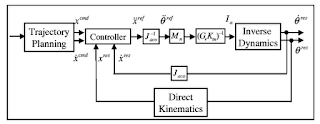
マニピュレータの制御は目標軌道と実際の軌道との偏差を直交座標空間上で計算し、逆運動学(逆ヤコビ行列)によって関節空間に変換して制御入力値とする．

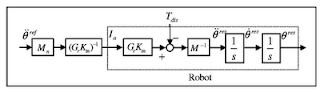
このシステムの場合、下図に示すようにプラント(マニピュレータ)への入力は加速度であり、加速度制御系を構成している． 図中の添え字〇_ｎはノミナル化したパラメータを示す．ノミナル化とは行列の対角成分のみを抽出することである．ここではトルク定数を不変とし、Ktn = Ktとみなして計算を行う.実際のシステムと比較した場合、このシステムのモデルにはモデル化誤差・パラメータ変動等が存在する．

関節モータも含めた全体の動力学

マニュピュレータ全体の運動を制御するためには第1章で考察したモータから関節にかかる力と第2章で考察して来たマニュピュレータの運動により関節に生じる力とを合成する必要がある． モータにおける外乱Tdisを考慮しないとき、関節モータの動力学を含めた全体の動力学は次のように表される．

ここで、Gr,Jm,Dは対角成分のみ0でない値を持つ定数行列である． また、上図におけるMnは初期姿勢のMとする．

シミュレーション結果

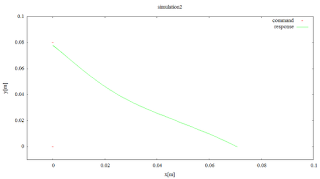
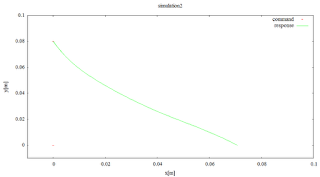
ステップ軌道

オブザーバー適用前

オブザーバー適用後

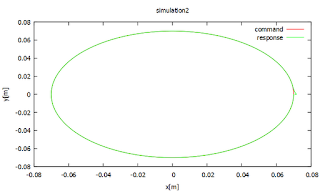
円軌道

オブザーバー適用前

オブザーバー適用後

オブザーバー適用前と適用後で、重力,コリオリ力などの外乱が補償できている事が分かる。